Learning-based Surrogates for Complex Physics
Reducing the computational cost of first-principle simulations by introducing machine learning for complex physics.
Learned Multiphysics and Differentiable Simulation
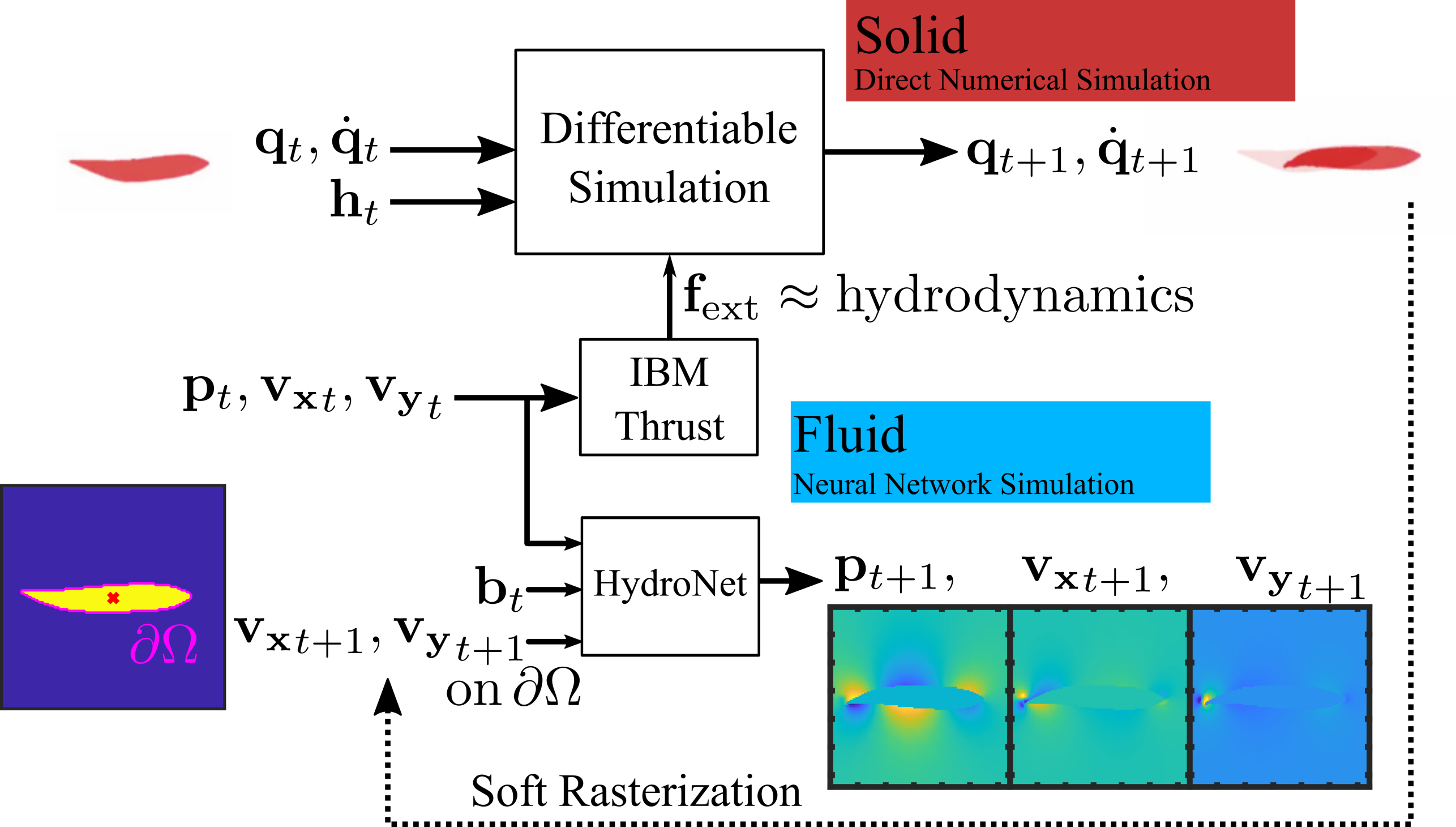
We are developing multiphysics simulation techniques, leveraging insights from both numerical simulation and Physics-Informed Neural Networks, with the goal of better modeling, designing and controlling soft robots. Our latest work on the topic, "Fast Aquatic Swimmer Optimization with Differentiable Projective Dynamics and Neural Network Hydrodynamic Models", combines differentiable Finite Element Method simulation of the swimmer's soft body with a neural network-based surrogate model of the fluid medium which is fully learned in a self-supervised manner. We obtain a powerful, sufficiently general and fast simulator that can be used for design tasks where previous computationally intensive and non-differentiable methods could not be effectively employed. We demonstrate the computational efficiency and differentiability of our hybrid approach by finding the optimal swimming frequency of a simulated 2D soft body swimmer through gradient-based optimization, but exciting future applications of the technique could involve full 3D shape optimization, real world robotic fabrication, and the training of neural network based controllers without expensive Reinforcement Learning.
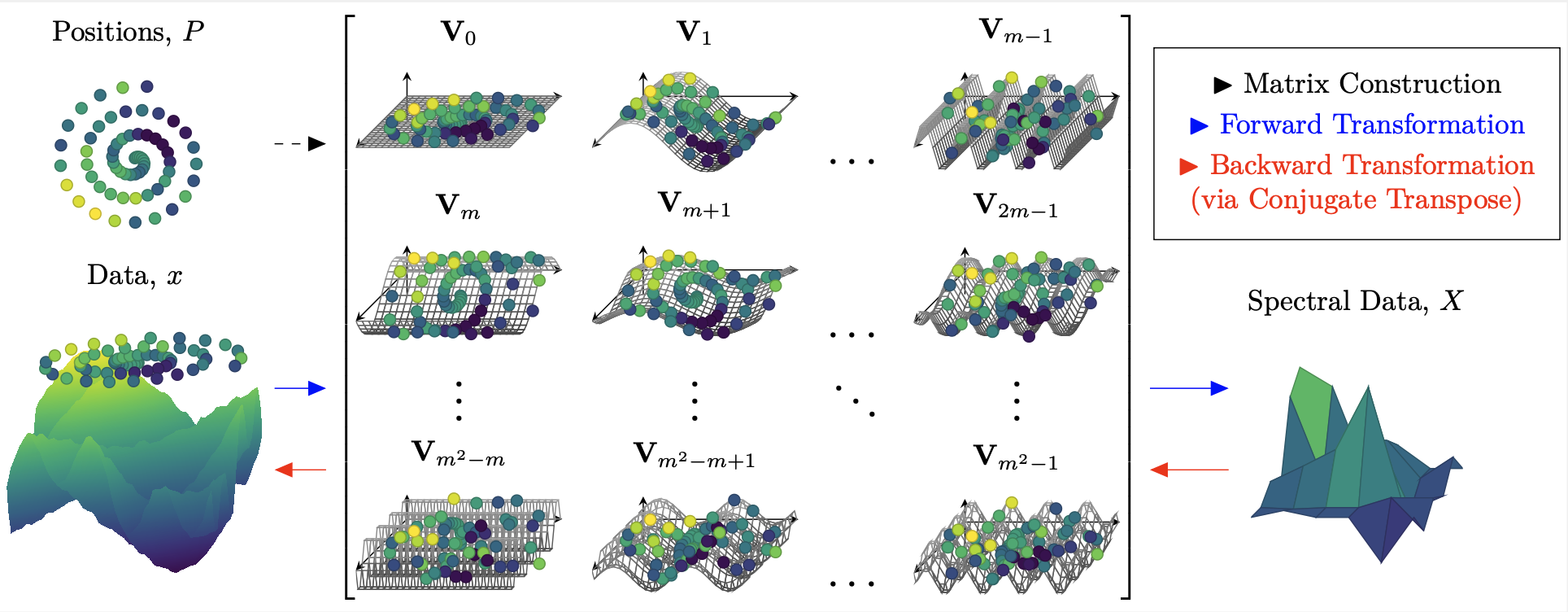
Beyond Regular Grids: Fourier-Based Neural Operators on Arbitrary Domains
The computational efficiency of many neural op- erators, widely used for learning solutions of PDEs, relies on the fast Fourier transform (FFT) for performing spectral computations. As the FFT is limited to equispaced (rectangular) grids, this limits the efficiency of such neural operators when applied to problems where the input and output functions need to be processed on general non-equispaced point distributions. Leveraging the observation that a limited set of Fourier (Spectral) modes suffice to provide the required expressivity of a neural operator, we propose a simple method, based on the efficient direct evaluation of the underlying spectral transformation, to extend neural operators to arbitrary domains. An efficient implementation of such direct spectral evaluations is coupled with existing neural operator models to allow the processing of data on arbitrary non-equispaced distributions of points. With extensive empirical evaluation, we demonstrate that the proposed method allows us to extend neural operators to arbitrary point distributions with significant gains in training speed over baselines while retaining or improving the accuracy of Fourier neural operators (FNOs) and related neural operators.